Creating a Hierarchical State Automaton
Hierarchical State Automatons ("HSA") are an extension of State Automatons whose states can themselves contain state automatons.
Note that HSAs are experimental, thus not all features of state automata are supported. In particular, the support for verification is limited (e.g., reachability analysis is not supported). The simulation of HSAs is possible.
When to use HSAs?
HSAs are useful when a usual state automaton becomes too big to be handled conveniently. In this case, one can often decompose the state automaton into a HSA. Note that HSAs are not more powerful than state automata, i.e., one cannot use a HSA to model a behavior which cannot be modeled by a state automaton.
Create a Hierarchical State Automaton
To create a HSA, simply model the top state automaton like any other automaton:

Then simply drag&drop a state from the Model Elements View to some existing state of your diagram:
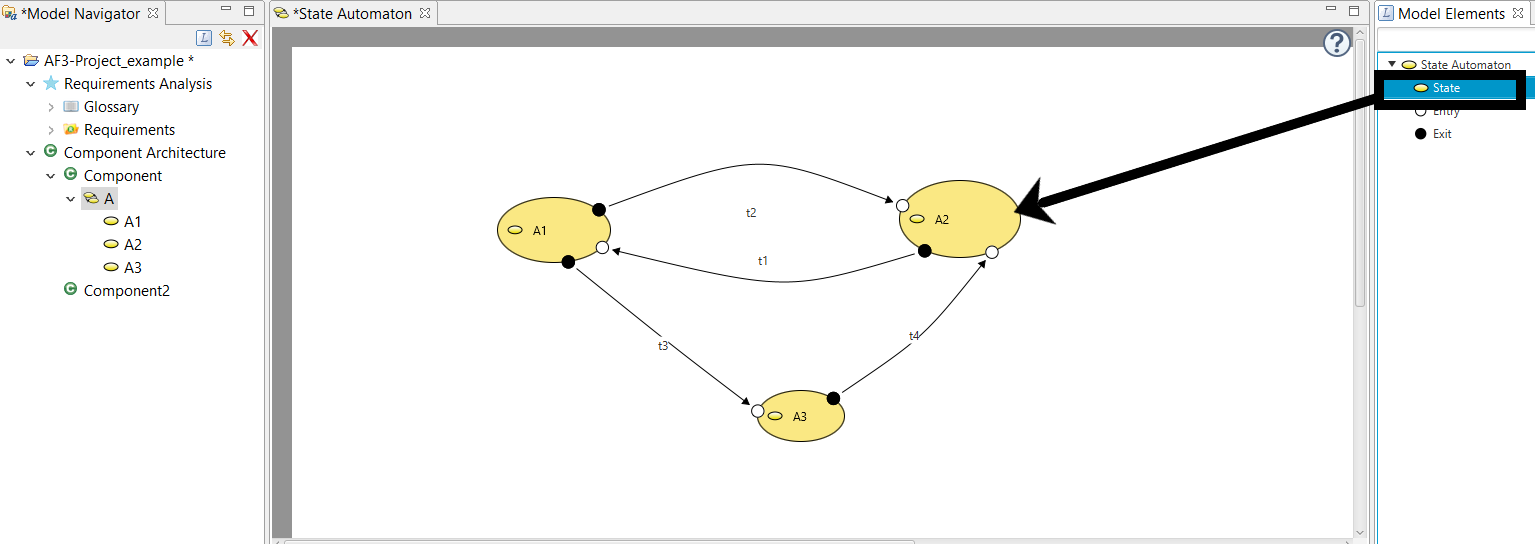
This will create a state automaton inside the existing state:

You can then double click the state to open this inner automaton:

And start building the inside automaton as any state automaton:

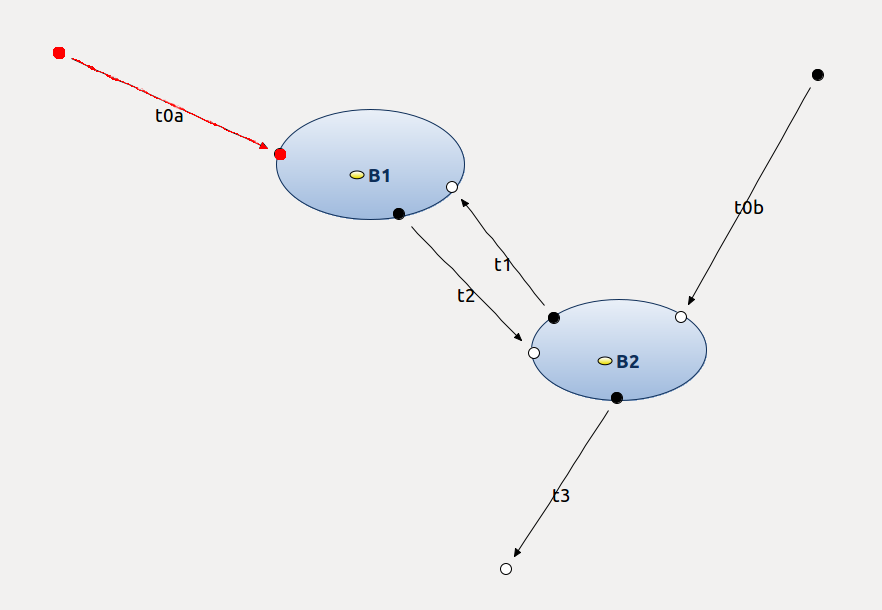
When modeling the inner automaton, one can notice that some ports are automatically added, disconnected from any state. See, e.g., Input, Input1, and Output below:

Just as any other port, these ports can be connected to the states, thus allowing to make a connection between the behavior of the inner state automaton and the outer state automaton.
Semantics and Behavior of the Inner Automaton
The inner automaton is connected to the outer one through the ports of the outer state. The semantics of the HSA are as follows: assume a transition followed in the outer state automaton goes to a hierarchical state through some port "Input":

Then the focus switches to the inside automaton by following any suitable transition from "Input":
Once inside this automaton, the usual behavior of state automaton applies. Note that, meanwhile, the outer automaton is "frozen" in its current state. This is until an output port is reached in the inner automaton:
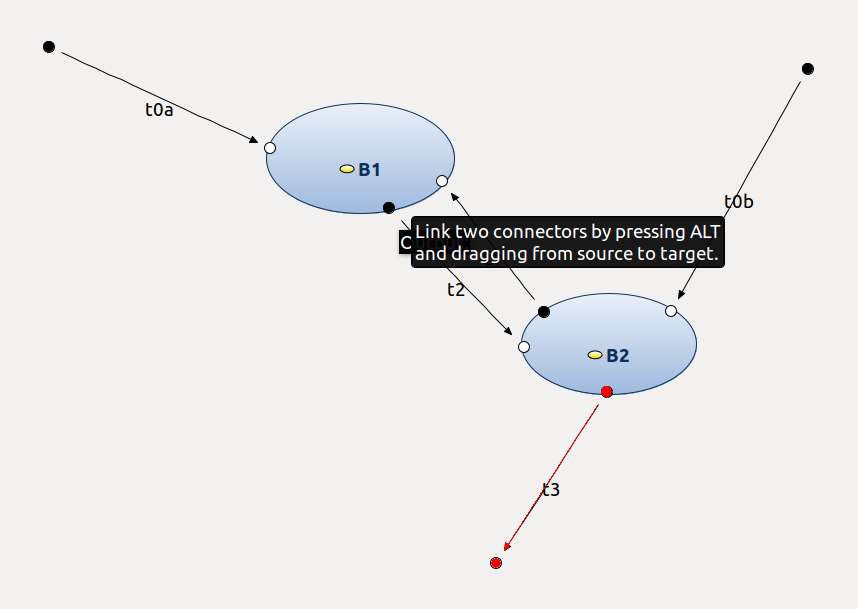
In that case the focus gets back to the outer automaton, which follows the appropriate transition: